正式名「あるかりがメモレベルで理解不能なことを書くブログ」
No.206 クロスワードの盤面にカギの数字を入れよう!
Category : 今週のパズル
以前、
「クロスワードのカギ番号をつけるプログラムがなくなった」
という話がありましたが、この度、会社の仕事でVBを学ぶことになり、
VBの勉強になるなぁと習作みたいな感じでそれを作り直していたら、
なんか「VBは要らないよ。それよりPHPをがんばれ」的な
ことを言われたので、じゃあ
PHPの勉強になるなぁと習作みたいな感じで作り直してみたのですが、
なんか「PHPも要らないよ」的な話になってきたので、
腹が立って
ナゼかジャバスクリプトで作ってみた。
(http://brandk.net/alk/sozai/cross/index.html)
むしゃくしゃしてやった。コード最適化はしていない。
以下、欠点。
・InternetExplorer7.0.5730.13とFirefoxで6.3.6で動いたが
Netscape7.1で動かなかった。別に対応する予定はない。
・タテ25xヨコ15で点対称オプションをつけると
InternetExplorer7でさすがに反応が遅い。が、我慢しろ。
・説明とか決してユーザーフレンドリーではない。
「習うより慣れろ」を実践して下さい。
・ブラウザによっては、再表示しても点対称の値が戻らなかったり
するので、力技でガチャガチャやってください。
・もっと良いコードが書ける方は、web上にアップした上で
こっそりURLを教えてください。
「クロスワードのカギ番号をつけるプログラムがなくなった」
という話がありましたが、この度、会社の仕事でVBを学ぶことになり、
VBの勉強になるなぁと習作みたいな感じでそれを作り直していたら、
なんか「VBは要らないよ。それよりPHPをがんばれ」的な
ことを言われたので、じゃあ
PHPの勉強になるなぁと習作みたいな感じで作り直してみたのですが、
なんか「PHPも要らないよ」的な話になってきたので、
腹が立って
ナゼかジャバスクリプトで作ってみた。
(http://brandk.net/alk/sozai/cross/index.html)
むしゃくしゃしてやった。コード最適化はしていない。
以下、欠点。
・InternetExplorer7.0.5730.13とFirefoxで6.3.6で動いたが
Netscape7.1で動かなかった。別に対応する予定はない。
・タテ25xヨコ15で点対称オプションをつけると
InternetExplorer7でさすがに反応が遅い。が、我慢しろ。
・説明とか決してユーザーフレンドリーではない。
「習うより慣れろ」を実践して下さい。
・ブラウザによっては、再表示しても点対称の値が戻らなかったり
するので、力技でガチャガチャやってください。
・もっと良いコードが書ける方は、web上にアップした上で
こっそりURLを教えてください。
PR
No.201 オモパ投稿
Category : 今週のパズル
オモパの投稿が終わりました。
他の作家さんのブログを巡回してみて、
ハタと気が付きましたが、
応援作も2軍のパズルも1問たりとも作ってませんでした。
まあいいや。
他の作家さんのブログを巡回してみて、
ハタと気が付きましたが、
応援作も2軍のパズルも1問たりとも作ってませんでした。
まあいいや。
No.198 日の目を見ずに
Category : 今週のパズル
オモパの清書に勤しんでおりましたところ、
古いオモパが出てきたので、陰干し。
・チェックポイント(オモパ)

(1)○から他の○まで破線上に直線をのばし、
すべての○を一本道でつなぎます。
(2)線は丸のない格子点上で交差することが
あります。その場合は立体交差とみなし、
交差する線を飛び越えます。
(3)盤面上の○を塗り、●にすることがあり
ます。●には線が通りません。
(4)同じ色の丸はタテヨコに連続しません。
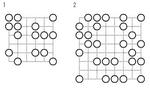

121号「アクセスポイント」の白丸と黒丸の関係に惚れ、
そこだけ抽出したら碁石拾いテイストが満載になった改作。
122号用に投稿したけど採用なし。
元ネタの要素を切り捨てすぎたのと、
入口が少なすぎるのが敗因とは思う。
(3)を「線が通らない○は●になります。」にして
(4)とまとめた方が良かったかな。
最初から●を表出するのはアリだと思う。
一本道よりループの方が良いような気もするけどなぁ。
古いオモパが出てきたので、陰干し。
・チェックポイント(オモパ)
(1)○から他の○まで破線上に直線をのばし、
すべての○を一本道でつなぎます。
(2)線は丸のない格子点上で交差することが
あります。その場合は立体交差とみなし、
交差する線を飛び越えます。
(3)盤面上の○を塗り、●にすることがあり
ます。●には線が通りません。
(4)同じ色の丸はタテヨコに連続しません。
121号「アクセスポイント」の白丸と黒丸の関係に惚れ、
そこだけ抽出したら碁石拾いテイストが満載になった改作。
122号用に投稿したけど採用なし。
元ネタの要素を切り捨てすぎたのと、
入口が少なすぎるのが敗因とは思う。
(3)を「線が通らない○は●になります。」にして
(4)とまとめた方が良かったかな。
最初から●を表出するのはアリだと思う。
一本道よりループの方が良いような気もするけどなぁ。
No.195 とおでして
Category : 今週のパズル
朝から運転免許証の更新に行って、
帰りにプリンターのカラーインクを買ってきました。
このカラーインクは、
黒インクの印刷がかすれたときのヘッドクリーニングでのみ使用され、
一度も紙に印刷されることのないまま寿命を全うするという
悲しい運命(さだめ)が待っています。
さて、これでオモパ原稿がきれいに印刷できるようになります。
帰りにプリンターのカラーインクを買ってきました。
このカラーインクは、
黒インクの印刷がかすれたときのヘッドクリーニングでのみ使用され、
一度も紙に印刷されることのないまま寿命を全うするという
悲しい運命(さだめ)が待っています。
さて、これでオモパ原稿がきれいに印刷できるようになります。
No.187 二乗数の事情通
Category : 今週のパズル
「たすくえあ」の紛れについて調べていたら、
ちょっとだけ面白いことを見つけました。
四角の中に9とあったら、「3x3の正方形1つ」または
「2x2の正方形2つと1x1の正方形1つ」と隣接します。
つまり、2種類パターンがあるということです。
「 3x3 = 2x2 + 2x2 + 1x1 」ですね。
複数の可能性があることを紛れと呼んでいます。私が。勝手に。
前者と後者で、最大となる正方形の一辺の長さの差が1なので
この状態を特に「差が1の紛れ」と呼んでいます。これも私が勝手に。
んで、ココから本題。
二乗数1つと2つの組み合わせになる『差が1の紛れ』のものを
( A^2 = B^2 + C^2 、または A^2 = B^2 + C^2 + 1 で、
かつ、A = B + 1 )
小さい順にいくつか羅列してみました。
この次の行は、もちろん「 113x113 = 112x112 + 15x15 」です。
もう1つ、
二乗数1つと2つの組み合わせになる『差が2の紛れ』のものを
( A^2 = B^2 + C^2 で、かつ、A = B + 2 )
(* A^2 = B^2 + C^2 + 1 のものは見つからなかったよ)
小さい順にいくつか羅列してみましょう。
この次の行は、もちろん「 101x101 = 99x99 + 20x20 」です。
(もし数学に詳しい方がこの記事を読んでいらっしゃいましたら
既に名前がつけられているであろうこの法則の名前をご教示願います)
特に「 101x101 = 99x99 + 20x20 」なんて数式は、
見ているだけでウットリしてしまいますね。すばらしいです。
なんとなくすげぇと感銘を受けたあなた!
ぜひタテ120マス、ヨコ120マス以上あるたすくえあを作って
この紛れを入れてみてくださいませ。私は心の底から応援します。
ちょっとだけ面白いことを見つけました。
四角の中に9とあったら、「3x3の正方形1つ」または
「2x2の正方形2つと1x1の正方形1つ」と隣接します。
つまり、2種類パターンがあるということです。
「 3x3 = 2x2 + 2x2 + 1x1 」ですね。
複数の可能性があることを紛れと呼んでいます。私が。勝手に。
前者と後者で、最大となる正方形の一辺の長さの差が1なので
この状態を特に「差が1の紛れ」と呼んでいます。これも私が勝手に。
んで、ココから本題。
二乗数1つと2つの組み合わせになる『差が1の紛れ』のものを
( A^2 = B^2 + C^2 、または A^2 = B^2 + C^2 + 1 で、
かつ、A = B + 1 )
小さい順にいくつか羅列してみました。
3x 3 = 2x 2 + 2x 2 + 1x 1何か面白そうな並びですね。ちょっと補足の行を足しましょう。
5x 5 = 4x 4 + 3x 3
9x 9 = 8x 8 + 4x 4 + 1x 1
13x13 = 12x12 + 5x 5
19x19 = 18x18 + 6x 6 + 1x 1
25x25 = 24x24 + 7x 7
・・・
1x 1 = 0x 0 + 1x 1おお!なんとなく美しいですね。
↓ 2 ↓ 2 ↓ 1 ↓+1
3x 3 = 2x 2 + 2x 2 + 1x 1
↓ 2 ↓ 2 ↓ 1 ↓-1
5x 5 = 4x 4 + 3x 3
↓ 4 ↓ 4 ↓ 1 ↓+1
9x 9 = 8x 8 + 4x 4 + 1x 1
↓ 4 ↓ 4 ↓ 1 ↓-1
13x13 = 12x12 + 5x 5
↓ 6 ↓ 6 ↓ 1 ↓+1
19x19 = 18x18 + 6x 6 + 1x 1
↓ 6 ↓ 6 ↓ 1 ↓-1
25x25 = 24x24 + 7x 7
↓ 8 ↓ 8 ↓ 1 ↓+1
33x33 = 32x32 + 8x 8 + 1x 1
↓ 8 ↓ 8 ↓ 1 ↓-1
41x41 = 40x40 + 9x 9
↓10 ↓10 ↓ 1 ↓+1
51x51 = 50x50 + 10x10 + 1x 1
↓10 ↓10 ↓ 1 ↓-1
61x61 = 60x60 + 11x11
↓12 ↓12 ↓ 1 ↓+1
73x73 = 72x72 + 12x12 + 1x 1
↓12 ↓12 ↓ 1 ↓-1
85x85 = 84x84 + 13x13
↓14 ↓14 ↓ 1 ↓+1
99x99 = 98x98 + 14x14 + 1x 1
この次の行は、もちろん「 113x113 = 112x112 + 15x15 」です。
もう1つ、
二乗数1つと2つの組み合わせになる『差が2の紛れ』のものを
( A^2 = B^2 + C^2 で、かつ、A = B + 2 )
(* A^2 = B^2 + C^2 + 1 のものは見つからなかったよ)
小さい順にいくつか羅列してみましょう。
5x 5 = 3x 3 + 4x 4これも行を足してみましょう。
10x10 = 8x 8 + 6x 6
17x17 = 15x15 + 8x 8
26x26 = 24x24 + 10x10
37x37 = 35x35 + 12x12
・・・
2x 2 = 0x 0 + 2x 2これも美しいですねぇ。
↓ 3 ↓ 3 ↓ 2
5x 5 = 3x 3 + 4x 4
↓ 5 ↓ 5 ↓ 2
10x10 = 8x 8 + 6x 6
↓ 7 ↓ 7 ↓ 2
17x17 = 15x15 + 8x 8
↓ 9 ↓ 9 ↓ 2
26x26 = 24x24 + 10x10
↓11 ↓11 ↓ 2
37x37 = 35x35 + 12x12
↓13 ↓13 ↓ 2
50x50 = 48x48 + 14x14
↓15 ↓15 ↓ 2
65x65 = 63x63 + 16x16
↓17 ↓17 ↓ 2
82x82 = 80x80 + 18x18
この次の行は、もちろん「 101x101 = 99x99 + 20x20 」です。
(もし数学に詳しい方がこの記事を読んでいらっしゃいましたら
既に名前がつけられているであろうこの法則の名前をご教示願います)
特に「 101x101 = 99x99 + 20x20 」なんて数式は、
見ているだけでウットリしてしまいますね。すばらしいです。
なんとなくすげぇと感銘を受けたあなた!
ぜひタテ120マス、ヨコ120マス以上あるたすくえあを作って
この紛れを入れてみてくださいませ。私は心の底から応援します。
